
M = zeros(3,3,3)M(:) = 1:numel(M)M1 = M(:,:)Įxplanation: The indices of the elements in the input matrix ‘M’ is redefined and created new input matrix M1 with the application of the colon operator. The colon operator can also be used to manipulate specific dimensions of the input array. Working with all the entries in specified dimensions In that case, MATLABapplies a scalar expansion for the left-hand side to be filled. A scalar value can also be used as the right-hand side operand in the assignment operation. The values from the right-hand side get assigned to the input array in the left-hand side in the form of a column vector. Note: In order to maintain the shape of the input array, the number of elements being assigning to the input array should be the same as the number of elements in the existing array input. The application of the assignment operator in the assignment operation on the input matrix, assures the shape of the array remains unchanged. Maintaining the shape of an array during assignment operation %Creating column vector using only colon operatorĪllthesame = isequal(M32vec, M32vecP, M32vecR)ģ. %Creating column vector using %permute method %Creating column vector using reshape method The colon operator can also be used with reshaping or permute functions to create a column vector.
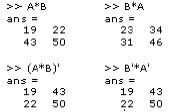
The colon operator can be used to transform the input of the row vector type to that of the column vector type. Creating a vector with only column format Using colon to create a listĪ vector with evenly-spaced numbers can be generated using a colon operator.Ģ. Application of MATLAB Colonīelow are the applications: 1. Example #6Įxplanation: The command has displayed the elements of the matrix ‘Mat_A’ indexed between 2 to 4. Example #3Įxplanation: The command has displayed the elements from the second row of the matrix ‘Mat_A’Įxplanation: The command has displayed the elements from the second column of the matrix ‘Mat_A’ Example #5Įxplanation: The command has displayed the elements of the matrix ‘Mat_A’ in a single column. Example #2Įxplanation: The command has generated list of values from -3 to 30 having different between 2 consecutive elements as ‘3’. īelow are some examples mentioned: Example #1Įxplanation: The command has generated a list of values from -3 to 3 having different between 2 consecutive elements as ‘1’. This results in a matrix having columns as. This syntax can be used to include the subscripts present in the first dimension and to use the vector having elements j:k, for indexing the second dimension. This syntax can be used to reshapethe elements of matrix ‘M’ into a matrix of two-dimensional.

This syntax can be used to store/extract the data from a three-dimensional array A set in the p th page. This syntax can be used to apply the vector list having the elementsj: kin order to index into matrix M. This syntax can be used to reshape the element ‘M’ into a vector containing a single column. This syntax is used to store the m throw of matrix M. This syntax is used to store the n th column of matrix M. This syntax is used to create a regularly-spaced vector list ‘li’ using values with increment value ‘i’, consisting of the elements. values with increment value ‘1’, consisting of the elements as. This syntax is used to create aunit spaced vector list i.e. My doubt is about how could I represent this function: randperm (N, M) from MATLAB/GNU Octave or np.random.permutation from Python in a mathematical notation? I know that $N$, $M$ are about $n$ cols and $m$ rows respectively and I saw in wikipedia that authors represented matrix permutation as $)$.Hadoop, Data Science, Statistics & others


 0 kommentar(er)
0 kommentar(er)
